In recent times, it has become quite difficult for students to study strategically and earn their desired goals. Not having appropriate guidance is one of the key factors responsible for students lagging in their curriculum. One of the subjects which kids, in general, find difficult and boring is Maths. Solving math problems and equations already are challenging and to top it off, it is not utterly their favorite subject. It can be strenuous to prepare for a math exam altogether.
A Geometric mean is one of the sub-parts of maths that can be a little tricky to solve. Various online platforms provide guidance and clarity to solve geometric mean problems.
Cuemath is an online learning platform that provides classes and worksheets for all your maths queries. It is quite practical and simple to use this website. All the worksheets are separated based on grades and topics, which makes it effortless and a time-saver to find what you are looking for.
Other Recommended Articles:
QuickBooks Install Diagnostic Tool – Download & Usage
QuickBooks Company File : Different Operations Performs On It
How to Cancel & Reactivate QuickBooks Online Subscription
What does geometric mean?
Geometric means an important part of statistics and mathematics. The basic aspects of statistics are mean, median and, mode. There are three types of means, mainly arithmetic mean, geometric mean, and harmonic mean. In geometric means, the given data values are multiplied, followed by finding the root with the radical index for the product of the values.
Formula of geometric mean:
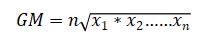
Where x1, x2 … are the data values.
It can also be expressed as:
Where n= f1+f2+… fn
Uses of geometric mean:
● Using geometric means allows the analysts to calculate and be up-to-date with the interests of the investments also called the compound interests.
1. Geometric means is a better way of calculating average return than the arithmetic mean, since AM can be a cumbersome process.
2. For a longer period of time, the arithmetic mean does not provide correct calculations of average return as it simply adds all the results and divides them with the total number of periods.
3. is the formula for calculating the average return through geometric mean.
4. It is used by analysts when calculating a sum of similar investments and interests, specifically for compounded interests.
● Geometric means are used in biological studies like the cell division and the growth rate.
1. In the biological study, it is used for data that is multiplicative.
2. Since it calculates growth rate if any value is negative or zero, the geometric mean will be undefined.
3. For instance, if we calculate the growth rate of a tree in three years, considering 14%, 6%, 2% to be the growth rates respectively. The final height can be calculated by taking the geometric mean of the numbers and multiplying it 3 times with itself.
4. Arithmetic means cannot be used, since it does not provide the correct end results.
5. Calculations with Geometric mean are made simple when dealing with a large sums of numbers.
● Geometry in mathematics has a special theorem to solve the right angled triangle and ellipse that is known as geometry mean theorem.
1. For a right-angled triangle, if the hypotenuse is divided into 2 segments from the line extending from the vertex with 90°, then the altitude of the line is equal to the geometric mean of the segments formed from the line.
2. For an ellipse, the semi-major and semi-minor axis can be calculated with the geometric mean of the distance of center from either focus and the geometric mean of max and min distances of the ellipse from a focus respectively.
Some important points of geometric mean:
1. The square of geometric means is equal to the product of the arithmetic mean and harmonic mean.
2. The product of the data values and the product of their geometric mean is the same.
3. The ratio of corresponding observations of the GM in two series is equal to the ratio of their geometric mean.